Machine Thinking - Machine Learning Models for Professionals

Machine learning comes in many flavours. In Foundations of Machine Learning we’ve seen lots of examples of parametric machine learning models, those where we take a guess at the form of the function mapping inputs to outputs. In this course, we are going to step things up a gear by forming a toolkit of non-parametric models.

So, what are non-parametric models? They simply give the machine learning algorithm the freedom to find the function that best fits the data. These models are naturally flexible and can be applied to different types of dataset.

As we build up a toolkit of advanced models, we’ll naturally consider the following topics:

Feature extraction, non-parametric modelling, decision surface analysis, Lagrangian manipulation, data splitting, and ensembles.

These are a few of the big concepts which we shall unpack in this course. They lay the foundation for many pattern recognition techniques used by professionals in modern-day research - they also help form some of the most powerful modelling tools we have to date.

In this course, you’ll get to grips with:

• Non-parametric models, unlocking their advanced predictive power over parametric techniques.
• Implementing and tuning advanced machine learning techniques with detailed code walk-throughs,
• The theoretical grounding underpinning the techniques used, so you have the expertise to interpret model predictions and understand the structure.
• How to quickly build a data science pipeline using the advanced models in the course.

This course follows on neatly from where Tim left off in Foundations of Machine Learning. In Tim’s course we moved from zero to sixty and covered the basic ideas around machine learning practice. In this course, we are using this foundation to start applying some advanced professional-standard tools in order to get the best results.

Section 1: Don’t Be Fooled by the Kernel Trick.

We’ll start unpacking the notion of ‘non-parametric models’ with an excellent prototype:

Projecting data features into a high-dimensional space where a linear model can solve the task.

The kernel trick we play means we never have to write down the projection, nor solve for the associated high-dimensional parameter vector. The derivation starts in our comfort zone - linear regression - and cleanly delivers a non-parametric model capable of cheaply understanding difficult non-linear data.

In this section, we shall unpack this technique and inspect the various hyper-parameter and kernel functions that need to be selected for the problem at hand.

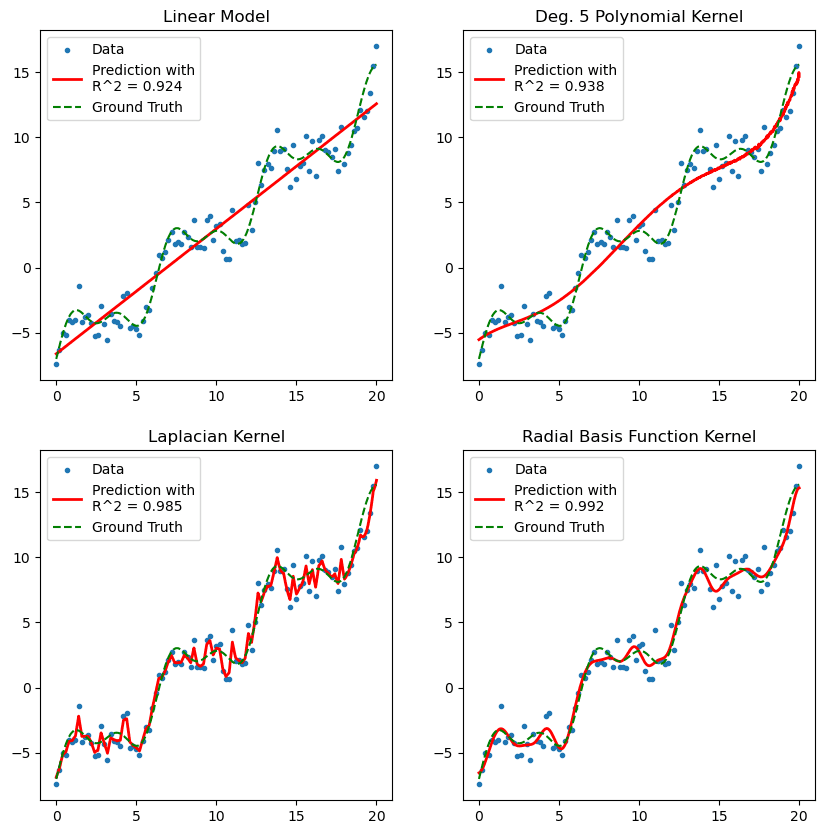
Figure 1. Relaxing a linear least-squares regression with the kernel trick allows for more general choices of predictive function.

Section 2: Support Vector Machines and They'll Support You.

One of the most powerful predictors and the cutting-edge of machine learning, before deep learning came along, Support Vector Machines are a valuable collection of models to keep in your toolkit. They can be applied to regression and classification tasks alike. Alongside the kernel trick, these become highly flexible, non-parametric machine learning algorithms that give unique insight to the most impactful data points in your training set; these are identified as support vectors.

We shall examine support vector machines for a range of tasks and visualise how support vectors may be identified within the model. Crucially, support vector machines are able to sparsify a dataset of many samples though selecting only those necessary to generate a predictive model.

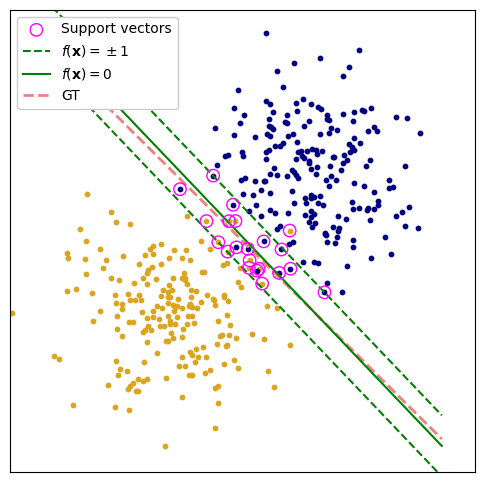
Figure 2. A linear SVM vs. a non-parametric 'kernel' SVM for predicting decision boundaries.

Section 3: Branch Out With Decision Trees.

If we want machines to think, shouldn't we apply some introspection first? How do we sift through information and make decisions? Consider a simple decision: "I'll cycle tomorrow, but only if the forecast is 60% likely to be dry". Based on what data? Weather forecasts. We choose our threshold (60%) and act accordingly in one of two ways. Of course, once taking the cycling option one may have many more decisions to make. What you'll see in this section is that a machine that can think in this way can very quickly and easily find optimal choices among a vast amount of data.

This is the basis of (dare I say "roots of") a decision tree. In this section, we shall unearth the mechanism by which they work and demonstrate their utility on a variety of problems. We'll discuss their pros and cons. Importantly, these simple models can be used as components of very effective models described in the next sections.

Section 4: Democracy Amongst Models with Ensembles.

When machine learning models such as the decision tree act alone they are vulnerable to over fitting to the original data they are shown. We know from experience that a fresh pair of eyes on a problem can help give new insight. So why not introduce more machine learning models to help each other out: an ensemble.

But how can ensembles of models give sensible predictions? How do we encode democracy? And, crucially, how can we deploy this technique to reduce over-fitting and improve model generalisation?

We shall answer these questions throughout this section whilst focussing on a typical ensemble technique: Random forests.

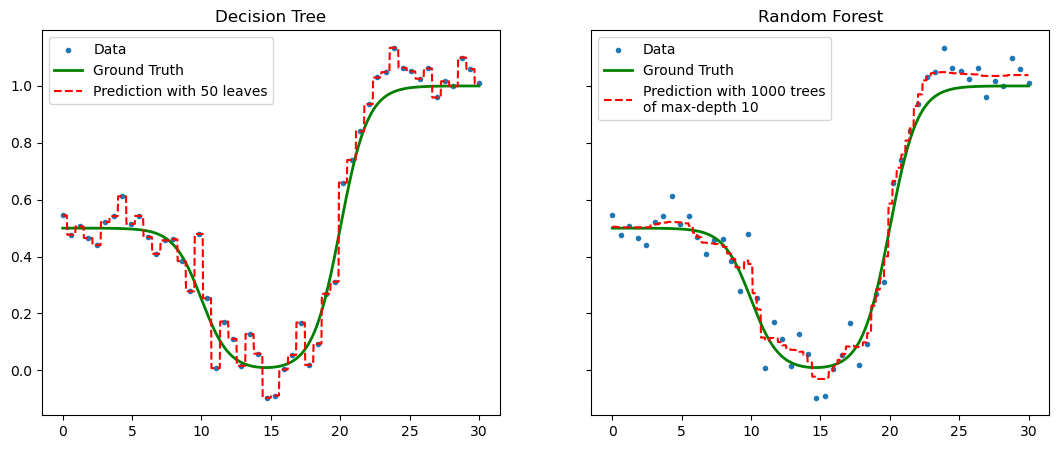
Figure 3. Overfitting in a decision tree can be interpolated by deploying a random forest.

Give Yourself a Gradient Boost.

Ensembles act as vast populations of independent models which participate in a democratic process to make advanced predictions.

But what if a collection of models all worked together from the start? One such technique, the jewel in the crown of our course, is known as 'Gradient Boosting'. Instead of all models predicting the target, each learns the error given in the previous. This means we can use far smaller models all working toward a common goal: reducing the error in our system.

In practice, this technique frequently outperforms all others. Perhaps the most successful tool in our toolbox is an advanced application of gradient boosting: XGBoost. In this section, we shall explore the ins and outs of gradient boosting as a technique as well as the application of XGBoost in the wild.

Dr Andy Corbett

Head of Research and Development, digiLab

Andy is most at home engaging in the mathematical rough & tumble of machine learning: brainstorming, coding, and designing deep learning models for explainable AI. He’s a keen cyclist and knows his way around a triathlon (even the wet bits). Andy likes strumming along to old blues tracks, cooking up new dishes, and if he could be anywhere he would be hiking with his family out on the Devon hills.